Describe the Method Used to Integrate Sine Cubed X.
I sec 3 x d x i First we break sec 3 x into sec. X cos x cos x d x Simplify.

Method 1 Integral Of Sin X Cos 3 X Substitution Youtube
In this tutorial we shall derive the integral of sine squared x.

. The integral of the secant cubed of X is of the form. Z 2xcosx2dx Z cosudu sinuC sinx2 C. Substitute x sin θ then dx cos θ dθ.
Choose the correct answer below. If the powers of both sine and cosine are odd either of the above methods can be used. X sin x d x x cos x cos x 1 d x Substitute.
Tanx C. Consider the integral. In the case of a right circular cylinder soup can this becomes V πr2h.
Integral we can replace it by du. Sinx dx-cosx C. Displaystyle int sec 3xdx frac 1 2 sec xtan xln leftsec xtan xrightC.
Considering that for t π 2 π 2 the cosine is positive. X and sec 2 x and now the integral i becomes. We can use this method which can be considered as the reverse product rule by considering one of the two factors as the derivative of another function.
Sinx C. 1 sin2t cos2t. For sqrta2-x2 use x a sin theta For sqrta2x2 use xa tan theta For sqrtx2-a2 use xa sec theta After we use these substitutions well get an integral that is do-able.
X asint dx acost with t π 2 π 2 and use the trigonometric identity. Start your trial now. Now recall the trig identity cos 2 x sin 2 x 1 sin 2 x 1 cos 2.
F g dx. Integrating the third power of sin x or any odd power for that matter is an easy task unlike sin2 xdx which requires a little trick. Let u sin x then du cos x dx.
The integral of secant cubed is a frequent and challenging indefinite integral of elementary calculus. Putting it all together we get our final result. Note that substituting gx x 2 1 by u will not work as g x 2x is not a factor of the integrand.
This is similar to what I got but instead of cosine they had sine and they had the signs - switched. For the first integral. Check out a sample QA here.
Rewrite sin 3x as 1 - cos2x sin x then use the substitution u sin x. Want to learn more about integration by parts. In the first step we are going to split Sec³ x as sec x Sec² x.
X cos x cos x d x Simplify. X 1 6 s i n 6 x C. Sec 2 x dx.
Use cos x d x sin x C. Du -sin xdx. Integrate Sec3 x with respect to x.
Commonly encountered and tricky integral. Then we can use integration by parts of that function because we know the formula for the integration of secant square of X from previous tutorials. Let u cos x then du sin x dx.
Du sec x tan x dx dv Sec ² x. Let us make the substitution x tan θ then and dx sec 2 θ dθ. A2 x2 a2 a2sin2t.
Want to see the step-by-step answer. Power Rule n1 x n dx. U3 3 C.
V A h. Sec³ x dx Sec x Sec² x dx. C fx dx.
For the sin 3. Integral of secant cubed. X sin x d x x cos x cos x 1 d x Substitute.
Check out this video. All you have to do is write the expression as sin x text even power of sin rewrite the even power using the formula sin2 x 1-cos2 x and apply the substitution u cos x ie. Sinxdx cosx C.
We can thus antidifferentiate ie integrate the function any number of times with the antiderivative expression alternating between a cubic function of sine and a cubic function of cosine. First week only 499. The integral becomes.
2 x 2 we have. Depending on the function we need to integrate we substitute one of the following trigonometric expressions to simplify the integration. F xdx Rxa2 x2dx.
For the second integral using substitution. I 1 cos. Each cross-section of a.
F dx g dx. Rewrite sin 3x as tan 3x cos x then use the. If the power of sine is odd n 2k 1 save one sine factor and use the identity sin 2 x cos 2 x 1 to express the remaining factors in terms of cosine.
Sin 2 x cos 2 x 1 that is k 2 ksin x 2 kcos x 2. Calculus questions and answers. X n1 n1 C.
Describe the method used to integrate sinºx. 1 3 cos3x C. Describe the method used to integrate sin 3x Choose the correct answer below o A.
To calculate the volume of a cylinder then we simply multiply the area of the cross-section by the height of the cylinder. Consider this integral. This integral cannot be evaluated by the direct formula of integration so using the trigonometric identity of half angle sin 2 x 1 cos.
Use cos x d x sin x C. Let f x be a rational function of x and a2 x2. Describe the method used to integrate sin 3 x.
Another possibility for example is. X cos x sin x C. Sec 3 x d x 1 2 sec x tan x ln sec x tan x C.
X cos x sin x C. F - g dx. F dx - g dx.
See Integration by Parts. Rewrite sin 3x as sin 2x sin x then use a half angle formula to rewrite. This seemed to work but my book had 1 4 sin 4.
This is not the only way to do the algebra and typically there are many paths to the correct answer. Rewrite sin 3x as tan 3x cos 3x then use the substitution u. Let u cosx du sinxdx.
U sec x dv Sec² x. Rewrite sin 3x as 1-cos 2x sin x then use the substitution us cos x. Rewrite sin ºxas sin 2x sinx then use a.
Describe the method used to integrate sin3 x. The integration is of the form. Lets first notice that we could write the integral as follows sin 5 x d x sin 4 x sin x d x sin 2 x 2 sin x d x sin 5 x d x sin 4 x sin x d x sin 2 x 2 sin x d x.
Since dudx 2x dx du2x and. The antiderivative of involves cos3 and cos both of which can be antidifferentiated and this now involves sin3 and sin. X d x I got 1 6 c o s x 6 1 4 c o s 4 x C.
Rewrite sin ºxas 1 - cos2x sin x then use the substitution u cos x. I sin 2 x d x. Integration by parts is a method to find integrals of products.

Integral Of X Sin X By Parts Youtube

Calculus Integral Int Sin X 3 Rm D X Mathematics Stack Exchange

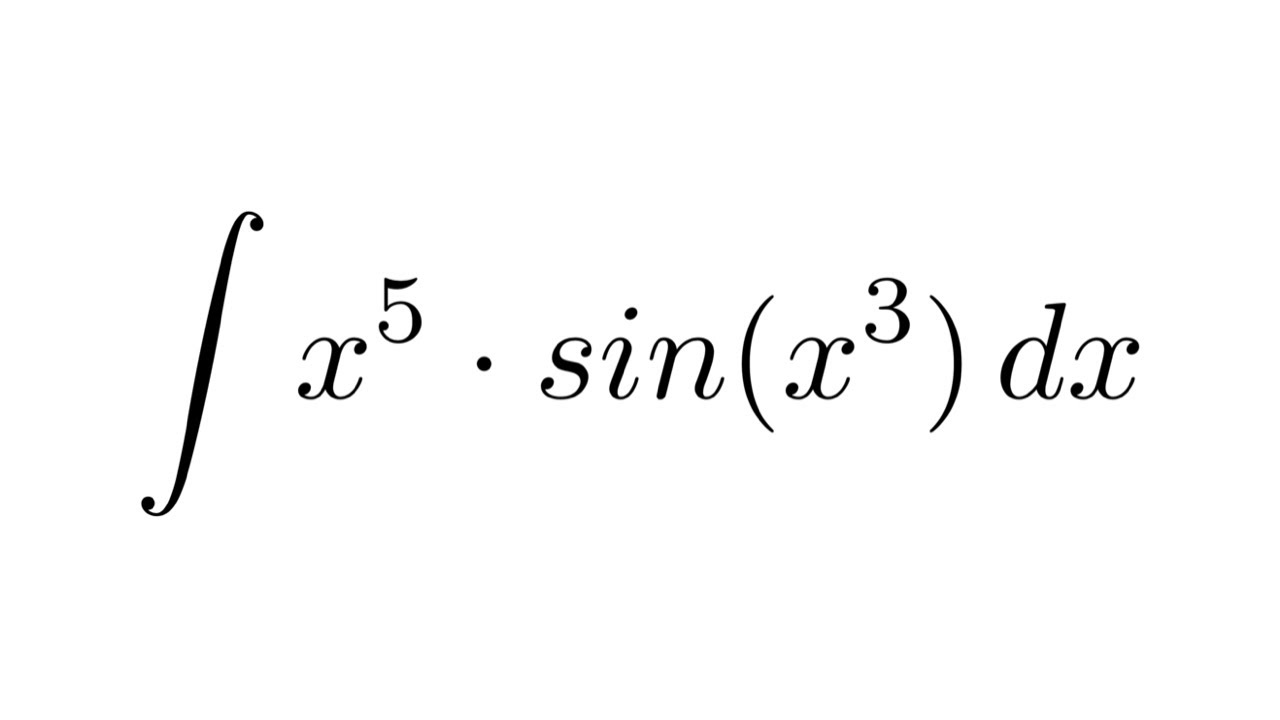
No comments for "Describe the Method Used to Integrate Sine Cubed X."
Post a Comment